一、 实验目的

1、 掌握函数的定义及调用方法

2、 掌握函数参数的传递（传值）、形参与实参的关系以及函数声明。

3、 理解局部变量的作用。

二、 实验内容

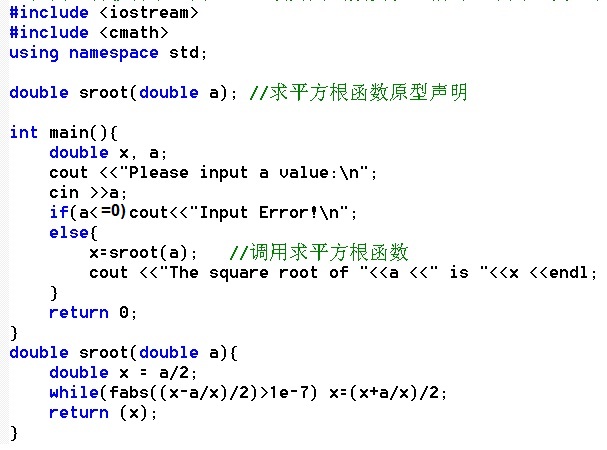
1、 将教材中【例2.12】改为用函数实现，编写一个用迭代法求平方根的函数。

【分析】 编写一个通用的求平方根的函数，参数（形参）为待求平方根的数，返回值为该数的平方根。

由于平方数不能为负数，因此在主调函数中，需要判断输入数的正、负，为正则用该参数（实参）调用求平方根函数；为负责输出错误信息。

【程序】

2、 设计一个简单的计算器程序，从键盘输入“+ 3 5 ”代表表达式“3+5”，程序读入运算符和数据，

调用Calculate( )函数，根据运算符进行加、减、乘、除四则运算。要求能反复执行这一过程，直到用户输入“#”符号作为运算符为止。

函数原型如下：

double add(double ,double ); //加

double minus(double ,double ); //减

double multi(double ,double ); //乘

double div(double ,double ); //除

double Calculate (double ,double ,char ); // 运算符作为字符数读入

3、 设计一个求两个数的最大公约数和最小公倍数的通用函数，要求能反复输入数据并输出其结果。

【提示】 可用枚举法，从两数中的小者开始尝试，并逐步往下取值，直到找到最大公约数。

4、歌德巴赫猜想指出：任何一个充分大的偶数都可以表示为两个素数之和。

例如： 4=2+2 6=3+3 8=3+5 10=3+7 10=5+5 … … 50=3+47 将4 -50之间的所有偶数用两个素数之和表示。判断一个整数是否为素数用函数完成。